
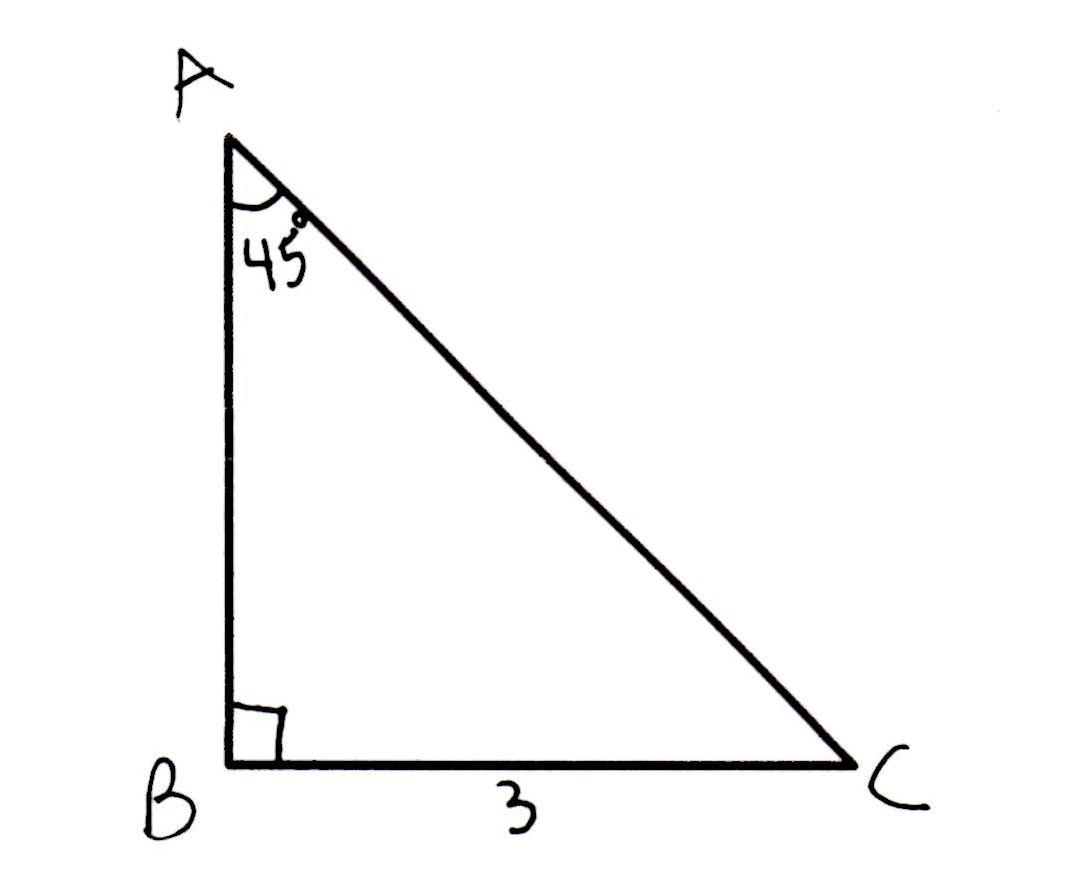
Get the free view of Chapter 10, Isosceles Triangles Concise Mathematics Class 9 ICSE additional questions for Mathematics Concise Mathematics Class 9 ICSE CISCE,Īnd you can use to keep it handy for your exam preparation. Maximum CISCE Concise Mathematics Class 9 ICSE students prefer Selina Textbook Solutions to score more in exams. Given: Area of right angled isosceles triangle 676 sq.cm Formula: Area of right angled isosceles triangle 1/2 × a × a. The questions involved in Selina Solutions are essential questions that can be asked in the final exam. Using Selina Concise Mathematics Class 9 ICSE solutions Isosceles Triangles exercise by students is an easy way to prepare for the exams, as they involve solutionsĪrranged chapter-wise and also page-wise. Selina textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.Ĭoncepts covered in Concise Mathematics Class 9 ICSE chapter 10 Isosceles Triangles are Isosceles Triangles, Isosceles Triangles Theorem, Converse of Isosceles Triangle Theorem. A width dx, then, should given you a cross-section with volume, and you can integrate dx and still be able to compute the area for the cross-section. You know the cross-section is perpendicular to the x-axis. Click hereto get an answer to your question Find the perimeter of an isosceles right - angled triangle having an area of 5000 m2. A couple of hints for this particular problem: 1. This will clear students' doubts about questions and improve their application skills while preparing for board exams.įurther, we at provide such solutions so students can prepare for written exams. Integrate along the axis using the relevant bounds. For a right-angled isosceles triangle, we have an isosceles triangle that has a right angle. An isosceles triangle is a triangle in which two sides of the triangle are equal. Selina solutions for Mathematics Concise Mathematics Class 9 ICSE CISCE 10 (Isosceles Triangles) include all questions with answers and detailed explanations. Area of Right Triangle (1/2 × base × height) (1/2 × Base × Perpendicular) Related Resources, Herons Formula Area of Triangle Right Angle Isosceles Triangle. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. has the CISCE Mathematics Concise Mathematics Class 9 ICSE CISCE solutions in a manner that help students Finally, solve the equation to find the unknown base, x. Then, use the Pythagorean theorem to create an equation involving x. Therefore, 0.6 m 2 = 0.Chapter 1: Rational and Irrational Numbers Chapter 2: Compound Interest (Without using formula) Chapter 3: Compound Interest (Using Formula) Chapter 4: Expansions (Including Substitution) Chapter 5: Factorisation Chapter 6: Simultaneous (Linear) Equations (Including Problems) Chapter 7: Indices (Exponents) Chapter 8: Logarithms Chapter 9: Triangles Chapter 10: Isosceles Triangles Chapter 11: Inequalities Chapter 12: Mid-point and Its Converse Chapter 13: Pythagoras Theorem Chapter 14: Rectilinear Figures Chapter 15: Construction of Polygons (Using ruler and compass only) Chapter 16: Area Theorems Chapter 17: Circle Chapter 18: Statistics Chapter 19: Mean and Median (For Ungrouped Data Only) Chapter 20: Area and Perimeter of Plane Figures Chapter 21: Solids Chapter 22: Trigonometrical Ratios Chapter 23: Trigonometrical Ratios of Standard Angles Chapter 24: Solution of Right Triangles Chapter 25: Complementary Angles Chapter 26: Co-ordinate Geometry Chapter 27: Graphical Solution (Solution of Simultaneous Linear Equations, Graphically) Chapter 28: Distance Formula To find the value of a base (x) in an isosceles triangle, first split the triangle into two congruent right triangles by drawing an altitude. The relation between square metres and square centimeters is defined as:ġ square meter = 10000 square centimeters

Therefore, we must convert this value into square meters. Now, note that we have been asked to find the area in square centimeters while the answer obtained above is in square meters. Each right triangle has an angle of, or in this case () (120) 60 degrees. Draw a line down from the vertex between the two equal sides, that hits the base at a right angle. Hence, the area of the given isosceles triangle = 48 cm 2 Example 9įind the area in square centimeters of the triangle whose base = 1.5 m and altitude = 0.8 m. Divide the isosceles into two right triangles. Applying Pythagoras theorem in ∆ABD, we have


 0 kommentar(er)
0 kommentar(er)
